
Aerodynamics

Aerodynamics (Ancient Greek: ἀήρ aero (air) + Ancient Greek: δυναμική (dynamics)) is the study of the motion of air, particularly when affected by a solid object, such as an airplane wing.[1] It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an important domain of study in aeronautics. The term aerodynamics is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891.[2] Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer simulations has formed a rational basis for the development of heavier-than-air flight and a number of other technologies. Recent work in aerodynamics has focused on issues related to compressible flow, turbulence, and boundary layers and has become increasingly computational in nature.

History
Modern aerodynamics only dates back to the seventeenth century, but aerodynamic forces have been harnessed by humans for thousands of years in sailboats and windmills,[3] and images and stories of flight appear throughout recorded history,[4] such as the Ancient Greek legend of Icarus and Daedalus.[5] Fundamental concepts of continuum, drag, and pressure gradients appear in the work of Aristotle and Archimedes.[6]

In 1726, Sir Isaac Newton became the first person to develop a theory of air resistance,[7] making him one of the first aerodynamicists. Dutch-Swiss mathematician Daniel Bernoulli followed in 1738 with Hydrodynamica in which he described a fundamental relationship between pressure, density, and flow velocity for incompressible flow known today as Bernoulli's principle, which provides one method for calculating aerodynamic lift.[8] In 1757, Leonhard Euler published the more general Euler equations which could be applied to both compressible and incompressible flows. The Euler equations were extended to incorporate the effects of viscosity in the first half of the 1800s, resulting in the Navier–Stokes equations.[9][10] The Navier–Stokes equations are the most general governing equations of fluid flow but are difficult to solve for the flow around all but the simplest of shapes.


In 1799, Sir George Cayley became the first person to identify the four aerodynamic forces of flight (weight, lift, drag, and thrust), as well as the relationships between them,[11][12] and in doing so outlined the path toward achieving heavier-than-air flight for the next century. In 1871, Francis Herbert Wenham constructed the first wind tunnel, allowing precise measurements of aerodynamic forces. Drag theories were developed by Jean le Rond d'Alembert,[13] Gustav Kirchhoff,[14] and Lord Rayleigh.[15] In 1889, Charles Renard, a French aeronautical engineer, became the first person to reasonably predict the power needed for sustained flight.[16] Otto Lilienthal, the first person to become highly successful with glider flights, was also the first to propose thin, curved airfoils that would produce high lift and low drag. Building on these developments as well as research carried out in their own wind tunnel, the Wright brothers flew the first powered airplane on December 17, 1903.

During the time of the first flights, Frederick W. Lanchester,[17] Martin Kutta, and Nikolai Zhukovsky independently created theories that connected circulation of a fluid flow to lift. Kutta and Zhukovsky went on to develop a two-dimensional wing theory. Expanding upon the work of Lanchester, Ludwig Prandtl is credited with developing the mathematics[18] behind thin-airfoil and lifting-line theories as well as work with boundary layers.


As aircraft speed increased designers began to encounter challenges associated with air compressibility at speeds near the speed of sound. The differences in airflow under such conditions lead to problems in aircraft control, increased drag due to shock waves, and the threat of structural failure due to aeroelastic flutter. The ratio of the flow speed to the speed of sound was named the Mach number after Ernst Mach who was one of the first to investigate the properties of the supersonic flow. Macquorn Rankine and Pierre Henri Hugoniot independently developed the theory for flow properties before and after a shock wave, while Jakob Ackeret led the initial work of calculating the lift and drag of supersonic airfoils.[19] Theodore von Kármán and Hugh Latimer Dryden introduced the term transonic to describe flow speeds between the critical Mach number and Mach 1 where drag increases rapidly. This rapid increase in drag led aerodynamicists and aviators to disagree on whether supersonic flight was achievable until the sound barrier was broken in 1947 using the Bell X-1 aircraft.

By the time the sound barrier was broken, aerodynamicists' understanding of the subsonic and low supersonic flow had matured. The Cold War prompted the design of an ever-evolving line of high-performance aircraft. Computational fluid dynamics began as an effort to solve for flow properties around complex objects and has rapidly grown to the point where entire aircraft can be designed using computer software, with wind-tunnel tests followed by flight tests to confirm the computer predictions. Understanding of supersonic and hypersonic aerodynamics has matured since the 1960s, and the goals of aerodynamicists have shifted from the behaviour of fluid flow to the engineering of a vehicle such that it interacts predictably with the fluid flow. Designing aircraft for supersonic and hypersonic conditions, as well as the desire to improve the aerodynamic efficiency of current aircraft and propulsion systems, continues to motivate new research in aerodynamics, while work continues to be done on important problems in basic aerodynamic theory related to flow turbulence and the existence and uniqueness of analytical solutions to the Navier–Stokes equations.

Fundamental concepts
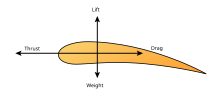
Understanding the motion of air around an object (often called a flow field) enables the calculation of forces and moments acting on the object. In many aerodynamics problems, the forces of interest are the fundamental forces of flight: lift, drag, thrust, and weight. Of these, lift and drag are aerodynamic forces, i.e. forces due to air flow over a solid body. Calculation of these quantities is often founded upon the assumption that the flow field behaves as a continuum. Continuum flow fields are characterized by properties such as flow velocity, pressure, density, and temperature, which may be functions of position and time. These properties may be directly or indirectly measured in aerodynamics experiments or calculated starting with the equations for conservation of mass, momentum, and energy in air flows. Density, flow velocity, and an additional property, viscosity, are used to classify flow fields.

Flow classification
Flow velocity is used to classify flows according to speed regime. Subsonic flows are flow fields in which the air speed field is always below the local speed of sound. Transonic flows include both regions of subsonic flow and regions in which the local flow speed is greater than the local speed of sound. Supersonic flows are defined to be flows in which the flow speed is greater than the speed of sound everywhere. A fourth classification, hypersonic flow, refers to flows where the flow speed is much greater than the speed of sound. Aerodynamicists disagree on the precise definition of hypersonic flow.

Compressible flow accounts for varying density within the flow. Subsonic flows are often idealized as incompressible, i.e. the density is assumed to be constant. Transonic and supersonic flows are compressible, and calculations that neglect the changes of density in these flow fields will yield inaccurate results.

Viscosity is associated with the frictional forces in a flow. In some flow fields, viscous effects are very small, and approximate solutions may safely neglect viscous effects. These approximations are called inviscid flows. Flows for which viscosity is not neglected are called viscous flows. Finally, aerodynamic problems may also be classified by the flow environment. External aerodynamics is the study of flow around solid objects of various shapes (e.g. around an airplane wing), while internal aerodynamics is the study of flow through passages inside solid objects (e.g. through a jet engine).

Continuum assumption
Unlike liquids and solids, gases are composed of discrete molecules which occupy only a small fraction of the volume filled by the gas. On a molecular level, flow fields are made up of the collisions of many individual of gas molecules between themselves and with solid surfaces. However, in most aerodynamics applications, the discrete molecular nature of gases is ignored, and the flow field is assumed to behave as a continuum. This assumption allows fluid properties such as density and flow velocity to be defined everywhere within the flow.

The validity of the continuum assumption is dependent on the density of the gas and the application in question. For the continuum assumption to be valid, the mean free path length must be much smaller than the length scale of the application in question. For example, many aerodynamics applications deal with aircraft flying in atmospheric conditions, where the mean free path length is on the order of micrometers and where the body is orders of magnitude larger. In these cases, the length scale of the aircraft ranges from a few meters to a few tens of meters, which is much larger than the mean free path length. For such applications, the continuum assumption is reasonable. The continuum assumption is less valid for extremely low-density flows, such as those encountered by vehicles at very high altitudes (e.g. 300,000 ft/90 km)[6] or satellites in Low Earth orbit. In those cases, statistical mechanics is a more accurate method of solving the problem than is continuum aerodynamics. The Knudsen number can be used to guide the choice between statistical mechanics and the continuous formulation of aerodynamics.

Conservation laws
The assumption of a fluid continuum allows problems in aerodynamics to be solved using fluid dynamics conservation laws. Three conservation principles are used:

- Conservation of mass
- Conservation of mass requires that mass is neither created nor destroyed within a flow; the mathematical formulation of this principle is known as the mass continuity equation.
- Conservation of momentum
- The mathematical formulation of this principle can be considered an application of Newton's Second Law. Momentum within a flow is only changed by external forces, which may include both surface forces, such as viscous (frictional) forces, and body forces, such as weight. The momentum conservation principle may be expressed as either a vector equation or separated into a set of three scalar equations (x,y,z components).
- Conservation of energy
- The energy conservation equation states that energy is neither created nor destroyed within a flow, and that any addition or subtraction of energy to a volume in the flow is caused by heat transfer, or by work into and out of the region of interest.
Together, these equations are known as the Navier–Stokes equations, although some authors define the term to only include the momentum equation(s). The Navier–Stokes equations have no known analytical solution and are solved in modern aerodynamics using computational techniques. Because computational methods using high speed computers were not historically available and the high computational cost of solving these complex equations now that they are available, simplifications of the Navier–Stokes equations have been and continue to be employed. The Euler equations are a set of similar conservation equations which neglect viscosity and may be used in cases where the effect of viscosity is expected to be small. Further simplifications lead to Laplace's equation and potential flow theory. Additionally, Bernoulli's equation is a solution in one dimension to both the momentum and energy conservation equations.

The ideal gas law or another such equation of state is often used in conjunction with these equations to form a determined system that allows the solution for the unknown variables.[20]

Branches of aerodynamics

Aerodynamic problems are classified by the flow environment or properties of the flow, including flow speed, compressibility, and viscosity. External aerodynamics is the study of flow around solid objects of various shapes. Evaluating the lift and drag on an airplane or the shock waves that form in front of the nose of a rocket are examples of external aerodynamics. Internal aerodynamics is the study of flow through passages in solid objects. For instance, internal aerodynamics encompasses the study of the airflow through a jet engine or through an air conditioning pipe.

Aerodynamic problems can also be classified according to whether the flow speed is below, near or above the speed of sound. A problem is called subsonic if all the speeds in the problem are less than the speed of sound, transonic if speeds both below and above the speed of sound are present (normally when the characteristic speed is approximately the speed of sound), supersonic when the characteristic flow speed is greater than the speed of sound, and hypersonic when the flow speed is much greater than the speed of sound. Aerodynamicists disagree over the precise definition of hypersonic flow; a rough definition considers flows with Mach numbers above 5 to be hypersonic.[6]

The influence of viscosity on the flow dictates a third classification. Some problems may encounter only very small viscous effects, in which case viscosity can be considered to be negligible. The approximations to these problems are called inviscid flows. Flows for which viscosity cannot be neglected are called viscous flows.

Incompressible aerodynamics
An incompressible flow is a flow in which density is constant in both time and space. Although all real fluids are compressible, a flow is often approximated as incompressible if the effect of the density changes cause only small changes to the calculated results. This is more likely to be true when the flow speeds are significantly lower than the speed of sound. Effects of compressibility are more significant at speeds close to or above the speed of sound. The Mach number is used to evaluate whether the incompressibility can be assumed, otherwise the effects of compressibility must be included.

Subsonic flow
Subsonic (or low-speed) aerodynamics describes fluid motion in flows which are much lower than the speed of sound everywhere in the flow. There are several branches of subsonic flow but one special case arises when the flow is inviscid, incompressible and irrotational. This case is called potential flow and allows the differential equations that describe the flow to be a simplified version of the equations of fluid dynamics, thus making available to the aerodynamicist a range of quick and easy solutions.[21]

In solving a subsonic problem, one decision to be made by the aerodynamicist is whether to incorporate the effects of compressibility. Compressibility is a description of the amount of change of density in the flow. When the effects of compressibility on the solution are small, the assumption that density is constant may be made. The problem is then an incompressible low-speed aerodynamics problem. When the density is allowed to vary, the flow is called compressible. In air, compressibility effects are usually ignored when the Mach number in the flow does not exceed 0.3 (about 335 feet (102 m) per second or 228 miles (366 km) per hour at 60 °F (16 °C)). Above Mach 0.3, the problem flow should be described using compressible aerodynamics.

Compressible aerodynamics
According to the theory of aerodynamics, a flow is considered to be compressible if the density changes along a streamline. This means that – unlike incompressible flow – changes in density are considered. In general, this is the case where the Mach number in part or all of the flow exceeds 0.3. The Mach 0.3 value is rather arbitrary, but it is used because gas flows with a Mach number below that value demonstrate changes in density of less than 5%. Furthermore, that maximum 5% density change occurs at the stagnation point (the point on the object where flow speed is zero), while the density changes around the rest of the object will be significantly lower. Transonic, supersonic, and hypersonic flows are all compressible flows.

Transonic flow
The term Transonic refers to a range of flow velocities just below and above the local speed of sound (generally taken as Mach 0.8–1.2). It is defined as the range of speeds between the critical Mach number, when some parts of the airflow over an aircraft become supersonic, and a higher speed, typically near Mach 1.2, when all of the airflow is supersonic. Between these speeds, some of the airflow is supersonic, while some of the airflow is not supersonic.


Supersonic flow
Supersonic aerodynamic problems are those involving flow speeds greater than the speed of sound. Calculating the lift on the Concorde during cruise can be an example of a supersonic aerodynamic problem.

Supersonic flow behaves very differently from subsonic flow. Fluids react to differences in pressure; pressure changes are how a fluid is "told" to respond to its environment. Therefore, since sound is, in fact, an infinitesimal pressure difference propagating through a fluid, the speed of sound in that fluid can be considered the fastest speed that "information" can travel in the flow. This difference most obviously manifests itself in the case of a fluid striking an object. In front of that object, the fluid builds up a stagnation pressure as impact with the object brings the moving fluid to rest. In fluid traveling at subsonic speed, this pressure disturbance can propagate upstream, changing the flow pattern ahead of the object and giving the impression that the fluid "knows" the object is there by seemingly adjusting its movement and is flowing around it. In a supersonic flow, however, the pressure disturbance cannot propagate upstream. Thus, when the fluid finally reaches the object it strikes it and the fluid is forced to change its properties – temperature, density, pressure, and Mach number—in an extremely violent and irreversible fashion called a shock wave. The presence of shock waves, along with the compressibility effects of high-flow velocity (see Reynolds number) fluids, is the central difference between the supersonic and subsonic aerodynamics regimes.

Hypersonic flow
In aerodynamics, hypersonic speeds are speeds that are highly supersonic. In the 1970s, the term generally came to refer to speeds of Mach 5 (5 times the speed of sound) and above. The hypersonic regime is a subset of the supersonic regime. Hypersonic flow is characterized by high temperature flow behind a shock wave, viscous interaction, and chemical dissociation of gas.

Associated terminology

The incompressible and compressible flow regimes produce many associated phenomena, such as boundary layers and turbulence.

Boundary layers
The concept of a boundary layer is important in many problems in aerodynamics. The viscosity and fluid friction in the air is approximated as being significant only in this thin layer. This assumption makes the description of such aerodynamics much more tractable mathematically.

Turbulence
In aerodynamics, turbulence is characterized by chaotic property changes in the flow. These include low momentum diffusion, high momentum convection, and rapid variation of pressure and flow velocity in space and time. Flow that is not turbulent is called laminar flow.

Aerodynamics in other fields
This section needs additional citations for verification. (March 2018) |
Engineering design
Aerodynamics is a significant element of vehicle design, including road cars and trucks where the main goal is to reduce the vehicle drag coefficient, and racing cars, where in addition to reducing drag the goal is also to increase the overall level of downforce.[21] Aerodynamics is also important in the prediction of forces and moments acting on sailing vessels. It is used in the design of mechanical components such as hard drive heads. Structural engineers resort to aerodynamics, and particularly aeroelasticity, when calculating wind loads in the design of large buildings, bridges, and wind turbines.

The aerodynamics of internal passages is important in heating/ventilation, gas piping, and in automotive engines where detailed flow patterns strongly affect the performance of the engine.

Environmental design
Urban aerodynamics are studied by town planners and designers seeking to improve amenity in outdoor spaces, or in creating urban microclimates to reduce the effects of urban pollution. The field of environmental aerodynamics describes ways in which atmospheric circulation and flight mechanics affect ecosystems.

Aerodynamic equations are used in numerical weather prediction.

Ball-control in sports
Sports in which aerodynamics are of crucial importance include soccer, table tennis, cricket, baseball, and golf, in which most players can control the trajectory of the ball using the "Magnus effect".

See also
- Aeronautics
- Aerostatics
- Aviation
- Insect flight – how bugs fly
- List of aerospace engineering topics
- List of engineering topics
- Nose cone design
- Fluid dynamics
- Computational fluid dynamics
References
- ^ Wragg, David W. (1974). A Dictionary of Aviation (1st American ed.). New York: Frederick Fell, Inc. p. 8. ISBN 0-85045-163-9.
- ^ "How the Stork Inspired Human Flight". flyingmag.com.[permanent dead link]
- ^ "Wind Power's Beginnings (1000 BC – 1300 AD) Illustrated History of Wind Power Development". Telosnet.com. Archived from the original on 2010-12-02. Retrieved 2011-08-24.
- ^ Berliner, Don (1997). Aviation: Reaching for the Sky. The Oliver Press, Inc. p. 128. ISBN 1-881508-33-1.
- ^ Ovid; Gregory, H. (2001). The Metamorphoses. Signet Classics. ISBN 0-451-52793-3. OCLC 45393471.
- ^ a b c Anderson, John David (1997). A History of Aerodynamics and its Impact on Flying Machines. New York, NY: Cambridge University Press. ISBN 0-521-45435-2.
- ^ Newton, I. (1726). Philosophiae Naturalis Principia Mathematica, Book II.
- ^ "Hydrodynamica". Britannica Online Encyclopedia. Retrieved 2008-10-30.
- ^ Navier, C. L. M. H. (1827). "Memoire Sur les Lois du Mouvement des fluides". Mémoires de l'Académie des Sciences. 6: 389–440.
- ^ Stokes, G. (1845). "On the Theories of the Internal Friction of Fluids in Motion". Transactions of the Cambridge Philosophical Society. 8: 287–305.
- ^ "U.S Centennial of Flight Commission – Sir George Cayley". Archived from the original on 20 September 2008. Retrieved 2008-09-10.
Sir George Cayley, born in 1773, is sometimes called the Father of Aviation. A pioneer in his field, he was the first to identify the four aerodynamic forces of flight – weight, lift, drag, and thrust and their relationship. He was also the first to build a successful human-carrying glider. Cayley described many of the concepts and elements of the modern airplane and was the first to understand and explain in engineering terms the concepts of lift and thrust.
- ^ d'Alembert, J. (1752). Essai d'une nouvelle theorie de la resistance des fluides.
- ^ Kirchhoff, G. (1869). "Zur Theorie freier Flussigkeitsstrahlen". Journal für die reine und angewandte Mathematik. 1869 (70): 289–298. doi:10.1515/crll.1869.70.289. S2CID 120541431.
- ^ Rayleigh, Lord (1876). "On the Resistance of Fluids". Philosophical Magazine. 2 (13): 430–441. doi:10.1080/14786447608639132.
- ^ Renard, C. (1889). "Nouvelles experiences sur la resistance de l'air". L'Aéronaute. 22: 73–81.
- ^ Lanchester, F. W. (1907). Aerodynamics.
- ^ Prandtl, L. (1919). Tragflügeltheorie. Göttinger Nachrichten, mathematischphysikalische Klasse, 451–477.
- ^ Ackeret, J. (1925). "Luftkrafte auf Flugel, die mit der grosser also Schallgeschwindigkeit bewegt werden". Zeitschrift für Flugtechnik und Motorluftschiffahrt. 16: 72–74.
- ^ "Understanding Aerodynamics: Arguing from the Real Physics" Doug McLean John Wiley & Sons, 2012 Chapter 3.2 "The main relationships comprising the NS equations are the basic conservation laws for mass, momentum, and energy. To have a complete equation set we also need an equation of state relating temperature, pressure, and density..." https://play.google.com/books/reader?id=_DJuEgpmdr8C&printsec=frontcover&pg=GBS.PA191.w.0.0.0.151
- ^ a b Katz, Joseph (1991). Low-speed aerodynamics: From wing theory to panel methods. McGraw-Hill series in aeronautical and aerospace engineering. New York: McGraw-Hill. ISBN 0-07-050446-6. OCLC 21593499.
Further reading
General aerodynamics

- Anderson, John D. (2007). Fundamentals of Aerodynamics (4th ed.). McGraw-Hill. ISBN 978-0-07-125408-3. OCLC 60589123.
- Bertin, J. J.; Smith, M. L. (2001). Aerodynamics for Engineers (4th ed.). Prentice Hall. ISBN 0-13-064633-4. OCLC 47297603.
- Smith, Hubert C. (1991). Illustrated Guide to Aerodynamics (2nd ed.). McGraw-Hill. ISBN 0-8306-3901-2. OCLC 24319048.
- Craig, Gale (2003). Introduction to Aerodynamics. Regenerative Press. ISBN 0-9646806-3-7. OCLC 53083897.
Subsonic aerodynamics

- Katz, Joseph; Plotkin, Allen (2001). Low-Speed Aerodynamics (2nd ed.). Cambridge University Press. ISBN 0-521-66552-3. OCLC 43970751.
- Obert, Ed (2009). Aerodynamic Design of Transport Aircraft at Google Books. Delft; About practical aerodynamics in industry and the effects on design of aircraft. ISBN 978-1-58603-970-7.
Transonic aerodynamics

- Moulden, Trevor H. (1990). Fundamentals of Transonic Flow. Krieger Publishing Company. ISBN 0-89464-441-6. OCLC 20594163.
- Cole, Julian D; Cook, L. Pamela (1986). Transonic Aerodynamics. North-Holland. ISBN 0-444-87958-7. OCLC 13094084.
Supersonic aerodynamics

- Ferri, Antonio (2005). Elements of Aerodynamics of Supersonic Flows (Phoenix ed.). Dover Publications. ISBN 0-486-44280-2. OCLC 58043501.
- Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0. OCLC 11404735.
- Anderson, John D. (2004). Modern Compressible Flow. McGraw-Hill. ISBN 0-07-124136-1. OCLC 71626491.
- Liepmann, H. W.; Roshko, A. (2002). Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0. OCLC 47838319.
- von Mises, Richard (2004). Mathematical Theory of Compressible Fluid Flow. Dover Publications. ISBN 0-486-43941-0. OCLC 56033096.
- Hodge, B. K.; Koenig K. (1995). Compressible Fluid Dynamics with Personal Computer Applications. Prentice Hall. ISBN 0-13-308552-X. OCLC 31662199.
Hypersonic aerodynamics

- Anderson, John D. (2006). Hypersonic and High Temperature Gas Dynamics (2nd ed.). AIAA. ISBN 1-56347-780-7. OCLC 68262944.
- Hayes, Wallace D.; Probstein, Ronald F. (2004). Hypersonic Inviscid Flow. Dover Publications. ISBN 0-486-43281-5. OCLC 53021584.
History of aerodynamics

- Chanute, Octave (1997). Progress in Flying Machines. Dover Publications. ISBN 0-486-29981-3. OCLC 37782926.
- von Karman, Theodore (2004). Aerodynamics: Selected Topics in the Light of Their Historical Development. Dover Publications. ISBN 0-486-43485-0. OCLC 53900531.
- Anderson, John D. (1997). A History of Aerodynamics: And Its Impact on Flying Machines. Cambridge University Press. ISBN 0-521-45435-2. OCLC 228667184.
Aerodynamics related to engineering

Ground vehicles

- Katz, Joseph (1995). Race Car Aerodynamics: Designing for Speed. Bentley Publishers. ISBN 0-8376-0142-8. OCLC 181644146.
- Barnard, R. H. (2001). Road Vehicle Aerodynamic Design (2nd ed.). Mechaero Publishing. ISBN 0-9540734-0-1. OCLC 47868546.
Fixed-wing aircraft

- Ashley, Holt; Landahl, Marten (1985). Aerodynamics of Wings and Bodies (2nd ed.). Dover Publications. ISBN 0-486-64899-0. OCLC 12021729.
- Abbott, Ira H.; von Doenhoff, A. E. (1959). Theory of Wing Sections: Including a Summary of Airfoil Data. Dover Publications. ISBN 0-486-60586-8. OCLC 171142119.
- Clancy, L.J. (1975). Aerodynamics. Pitman Publishing Limited. ISBN 0-273-01120-0. OCLC 16420565.
Helicopters

- Leishman, J. Gordon (2006). Principles of Helicopter Aerodynamics (2nd ed.). Cambridge University Press. ISBN 0-521-85860-7. OCLC 224565656.
- Prouty, Raymond W. (2001). Helicopter Performance, Stability, and Control. Krieger Publishing Company Press. ISBN 1-57524-209-5. OCLC 212379050.
- Seddon, J.; Newman, Simon (2001). Basic Helicopter Aerodynamics: An Account of First Principles in the Fluid Mechanics and Flight Dynamics of the Single Rotor Helicopter. AIAA. ISBN 1-56347-510-3. OCLC 47623950.
Missiles

- Nielson, Jack N. (1988). Missile Aerodynamics. AIAA. ISBN 0-9620629-0-1. OCLC 17981448.
Model aircraft

- Simons, Martin (1999). Model Aircraft Aerodynamics (4th ed.). Trans-Atlantic Publications, Inc. ISBN 1-85486-190-5. OCLC 43634314.
Related branches of aerodynamics

Aerothermodynamics

- Hirschel, Ernst H. (2004). Basics of Aerothermodynamics. Springer. ISBN 3-540-22132-8. OCLC 228383296.
- Bertin, John J. (1993). Hypersonic Aerothermodynamics. AIAA. ISBN 1-56347-036-5. OCLC 28422796.
Aeroelasticity

- Bisplinghoff, Raymond L.; Ashley, Holt; Halfman, Robert L. (1996). Aeroelasticity. Dover Publications. ISBN 0-486-69189-6. OCLC 34284560.
- Fung, Y. C. (2002). An Introduction to the Theory of Aeroelasticity (Phoenix ed.). Dover Publications. ISBN 0-486-49505-1. OCLC 55087733.
Boundary layers

- Young, A. D. (1989). Boundary Layers. AIAA. ISBN 0-930403-57-6. OCLC 19981526.
- Rosenhead, L. (1988). Laminar Boundary Layers. Dover Publications. ISBN 0-486-65646-2. OCLC 17619090.
Turbulence

- Tennekes, H.; Lumley, J. L. (1972). A First Course in Turbulence. The MIT Press. ISBN 0-262-20019-8. OCLC 281992.
- Pope, Stephen B. (2000). Turbulent Flows. Cambridge University Press. ISBN 0-521-59886-9. OCLC 174790280.
External links
- NASA's Guide to Aerodynamics. Archived 2012-07-15 at the Wayback Machine.
- Aerodynamics for Students
- Aerodynamics for Pilots (archived)
- Aerodynamics and Race Car Tuning (archived)
- Aerodynamic Related Projects. Archived 2018-12-13 at the Wayback Machine.
- eFluids Bicycle Aerodynamics. Archived 2009-12-15 at the Wayback Machine.
- Application of Aerodynamics in Formula One (F1) (archived)
- Aerodynamics in Car Racing. Archived 2009-12-06 at the Wayback Machine.
- Aerodynamics of Birds. Archived 2010-03-24 at the Wayback Machine.
- NASA Aerodynamics Index
See what we do next...
OR
By submitting your email or phone number, you're giving mschf permission to send you email and/or recurring marketing texts. Data rates may apply. Text stop to cancel, help for help.
Success: You're subscribed now !
